Cluster Analysis

Up above us all so high...

In the first part of this tutorial we shall imagine ourselves in a satellite taking photographs of the earth. In the process we shall learn some image processing as well as some clustering techniques.

A satellite image

This shows part of a blue ocean and two land masses with some green vegetation. We can recognize these by the color. A human eye is extremely adept at detecting large regions of similar colors in an image. A camera, however, has no such ability. It merely scans a scene in a mechanical way, faithfully reporting every dot in it, but has no idea if the dots constitute any pattern or not. The above image, for example, is made of 3000 dots, arranged in a rectangle that is 75 dots wide and 40 dots high. Each dot, by the way, is called a pixel (a short form for "picture element"). The camera uses three filters: red, green and blue. The camera reports the red-ness, green-ness and blue-ness of each pixel. The numbers are from 0 to 255. Thus, a perfectly red dot will have red value 255, green value 0 and blue value 0. If you increase the green component the dot will appear yellowish (since red plus green light make yellow light).

The 3000 dots in our pictures, therefore, are just 9000 numbers to the satellite. It is better to think of them as 3000 points in 3D. Our eye could quickly group (or cluster) these 3000 points into two clusters: ocean and land. The ability to group a large number of points in d-dimensions into a relatively smaller number of classes is the aim of cluster analysis. The file sat.dat stores the data set for this image. Before going into the statistics let us learn how to turn these 3000 points into an image using R. First read the data.

dat = read.table("sat.dat")

Notice that this file has no header line, so we have the omitted the usual head=T option. We are told that the data file has 3 columns and 3000 rows of numbers. Each row is for a pixel, and the 3 columns are for red, green and blue, respectively. Let us assign these names to the columns.

names(dat) = c("red","green","blue")
attach(dat)

Next make a vector of colors, one color for each point.

mycol = rgb(red,green,blue,max=255)

The function rgb makes colors by combining red, green and blue values. The max specification means 255 is to be considered the highest value for each color.

Next we need to specify the size of the image. It is 75 pixels in width and 40 pixels in height.

rows = 1:75
columns = 1:40

So the 3000 points are actually arranged as a 40 by 75 matrix. (The height, 40, is the number of rows.)

z = matrix(1:3000,nrow=75)

Now we are ready to make the image.

image(rows,columns,z,col=mycol)

If you do not like to see the axes and labels, then you may remove them using

image(rows,columns,z,col=mycol,bty="n",yaxt="n",
   xaxt="n",xlab="",ylab="")

Based on the 3000 points the statistical brain of the satellite has to decide that is seeing two land masses peeping out from a vast blue ocean. And one important tool to achieve this is called clustering.

But before we go into it let us make a 3D scatterplot out of the 3 variables.

library(scatterplot3d) #Warning! It won't work unless
                       #scatterplot3d is installed.
                       #I mention this to explain how
                       #you may do it if you can download
                       #this (pretty large) package.
                       #Also, this package is readily available for
                       #only Windows. To use it in Linux, you have
                       #to download the source code and compile!
                       #But we shall see a work around for this soon.

scatterplot3d is a R package. But it may not be already available on your computer. Then you can download it from the internet using

install.packages("scatterplot3d")

This will first let you choose from a list of web repositories to download from. (Preferably choose a US-based repository as these contain more packages). The download and installation starts automatically (may be slow depending on your internet connection).

Alternatively, you may download the zip file for your package (after finding it out using Google, say) from the internet directly (using your favorite downloader) and then install it locally by the command

install.packages(choose.file()) #for Windows
install.packages(file.choose()) #for Linux

Then you can use:

scatterplot3d(red,green,blue,color=mycol)

One problem with scatterplot3d is that there is no simple way to specify the viewing angle. This is rectified in the small script scat3d.r, which you can download. Now use

source("scat3d.r")
scat3d(red,green,blue,col=mycol)

You can also turn the plot around specifying the angles theta and phi as follows.

scat3d(red,green,blue,col=mycol,theta = 20, phi=0)

Just a jumble of points, right? We shall apply a technique called k-means clustering to group the 3000 points into 2 clusters. Then later we shall learn how k-means clustering works.

k-means clustering

Apply the command

cl = kmeans(dat,2)

and see what kmeans has returned.

names(cl)
cl$clus

Each pixel is put into one of two clusters (called 1 and 2), and cl$clus tells us the cluster of each pixel. The centers of the two clusters are given by

cl$center

Now we shall make an image of the clustering result. We are going to have an image consisting of only two colors, one for each cluster. It is natural to choose the center as the representative color for a cluster.

c2 = rgb(cl$cen[,1],cl$cen[,2],cl$cen[,3],max=255)
c2

Next we have to wrap the long vector cl$clus in to a 75 by 40 matrix in order to make the image.

image(rows,columns, matrix(cl$clus,75,40),col=c2)

Do you think that the ocean is well-separated from the land?

What about adding some more details? For this we shall increase k to 3, say.

cl = kmeans(dat,3)
c3 = rgb(cl$cen[,1],cl$cen[,2],cl$cen[,3],max=255)
image(rows,columns, matrix(cl$clus,75,40),col=c3)

As you increase the number of clusters more and more details are added to the image. Notice that in our example the details get added to the land masses instead of the ocean which is just a flat uninteresting sheet of water.

How the k-means algorithm works

Consider the data set shown below. We can see that it has two clusters of points.

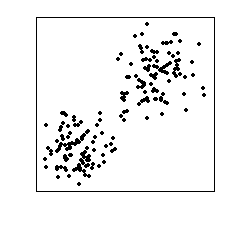Want to find the two clusters

In order to find these two clusters we shall employ the k-means algorithm with k=2.

The algorithm proceeds by alternating two steps that we shall call Monarchy and Democracy (see the figure below). In step 1, we apply Monarchy by choosing two random points as the kings of the two clusters. These two kings create their empires by enlisting the data points nearest to them as their subjects. So we get two kingdoms separated by the perpendicular bisector between the kings.

In step 2 we have Democracy, where the king is abolished and the data points in each kingdom choose their respective leaders as the average of themselves.

This election over, Monarchy kicks in once again as the elected leaders behave as kings, enlisting the nearest data points as subjects. This redefines the boundary of the kingdoms.

Then Democracy starts again, after which comes Monarchy. This process continues until the kingdoms do not change any more. These two kingdoms finally give the two clusters. The kings (or elected leaders) are the centers of the clusters.

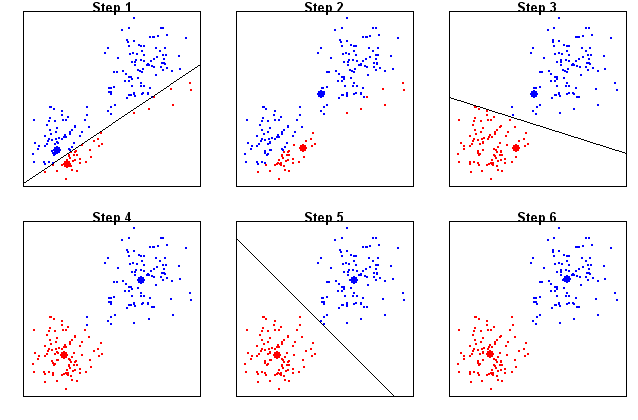Steps in the 2-means algorithm

Hierarchical clustering

Since the amount of details increases with a larger number of clusters, we come to the question ``How to choose the best number of clusters?" One way to resolve the issue is to first take a look at the results for all possible numbers of clusters. Clearly, if there are n cases in the data, then the number of clusters can go from 1 to n. This is the idea behind hierarchical clustering. It is like zooming down gradually on the details.

Consider the four shapes below.

Group these

Suppose that you are to group the similar shapes together making just two clusters. You'd most possibly put the two cubes in one cluster, while the sphere and the cone (both having round surfaces) will make the second cluster. So the two clusters are

(small cube, large cube) , (sphere, cone).

Next, suppose that you are to further split any one of the clusters (making three clusters in all). One natural way is to split the (sphere, cone) cluster into two separate clusters (sphere) and (cone) resulting in three clusters:

(small cube, large cube) , (sphere), (cone).

If we are to further increase the number of clusters, we have to split the first cluster:

(small cube), (large cube) , (sphere), cone).

And we have reached the maximum number of clusters. This step-by-step clustering process may be expressed using the following diagram which is sometimes called a clustering tree and sometimes called a dendrogram.

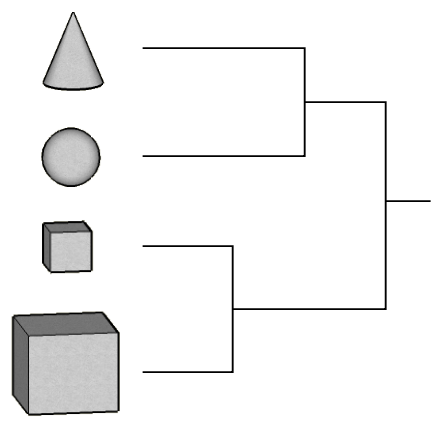Cluster tree

Note that this single tree contains information about all possible numbers of clusters.

An application

Here we shall illustrate an application of hierarchical clustering using the data set shapley.dat.

shap = read.table("shapley.dat",head=T)

dim(shap)
names(shap)

In this file we have some missing values for the variable Mag in column 3 that are coded as 0 (instead of NA). Let us convert these to NA

shap[shap[,3]==0,3] = NA
plot(shap,pch=".")

Now we shall perform hierarchical clustering, but we shall use only a subset of the data. We shall take only those cases where V is between 12000 and 16000. Also we shall consider only the three variables RA, DE and V.

attach(shap)
shap = shap[V>12000 & V<16000,c("RA","DE","V")]

Next we shall centre and scale each variable (i.e., we shall subtract the mean and divide by the standard deviation). This is conveniently done by the scale function.

shap = scale(shap)

In order to perform hierarchical clustering using the hclust function we have to find the distance matrix of the data. The (i,j)-th entry of this matrix gives the Euclidean distance between the i-th and the j-th point in the data set.

d = dist(shap)
mytree = hclust(d) #this may take some time
plot(mytree)

As we have mentioned earlier this hairy tree-like object (called a dendrogram) represents clustering allowing all possible numbers of clusters. In order to use it we have to ``cut'' it at a particular height as shown in the diagram below.

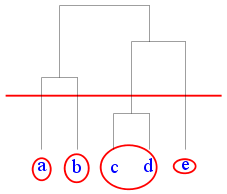Cutting a dendrogram

Suppose that we want 3 clusters for the Shapley data set. The dendrogram shows that we need to cut near height 6.

classes = cutree(mytree,h=6)
table(classes) #How many points in each class

Since we are working with 3D data (we have only 3 columns) so we can make a 3D scatterplot.

scatterplot3d(shap,color=classes)


	There are many clustering algorithms. In fact there is an entire R package called `cluster` devoted to clustering methods. Different clustering methods sometimes produce widely differing clusterings! One needs discretion and domain knowledge to choose one over the other.

Let us take a look at a method called AGglomerative NESting (AGNES).

library('cluster')

The R function that we shall employ is called agnes. We shall apply it on the Shapley data.

agn = agnes(shap) #this will take some time
plot(agn,which=2)

R can make two possible plots of the output from agnes. Here the argument which=2 requests the second of these. The returned object agn is a clustering tree somewhat like that returned by hclust. But the internal structures differ. So you cannot directly apply the cutree function to it. We first need to convert it to the structure compatible with hclust.

agnh = as.hclust(agn)
tmp = cutree(agnh,h=2.2)
table(tmp)

Here we have performed the cut at a specified height. We could also have specified the number of required clusters.

tmp2 = cutree(agnh,k=10)
table(tmp2)

You may recall the terms "single linkage","complete linkage" and "average linkage" from the theory class. What agnes uses by default is "average linkage". Let us see how "single linkage" performs for our data.

agn.sing = agnes(shap,method="single")
plot(agn.sing,which=2)

Exercise: Write an R script to split the Shapley data into 5 clusters using the "complete linkage" method of AGNES, and then make a 3D scatterplot of the data set using the colors red, green, blue, black and pink for the 5 clusters. [Solution]

k-nearest neighbors classification

This method is motivated by how a child is taught to read. The teacher first shows her some letters and tells her the names of the letters, so that she can associate the names with the shapes.

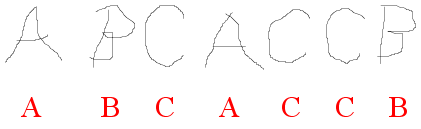The teacher's voice is shown in red

Then she is presented with some letters to see if she can identify them.

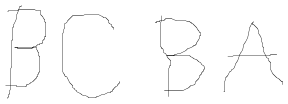The child is to identify these

When she sees a new letter the child quickly matches the new shape with the ones she has learned, and says the name of the letter that comes closest to the new letter.

Let us take a note of the different parts of this process. First, we have a training data set: the letter shapes and their names (shown in the first picture). Then we have a test data set which is very much like the training set, except that the names are not given.

We shall employ the same method to recognize the Hyades stars! We shall start with a training data set consisting of 120 stars of which the first 60 will be Hyades and the others not Hyades. We are supposed to learn to recognize a Hyades star based on these. Then we shall be given a test data set consisting of 56 new stars, some of which are Hyades (we are not told which). Our job will be to identify the Hyades stars in the test data sets. First download (right-click and save to your computer) the two data sets:train.dat and tst.dat. Next, load them into R.

trn = read.table("train.dat",head=T)
tst = read.table("tst.dat",head=T)
dim(trn)
dim(tst)

We are told that the first 60 stars in the training data set are Hyades, while the remaining 60 are not. So accordingly we shall make a vector of size 120:

trueClass = c(rep("Hyad",60),rep("NonHyad",60))
trueClass

Now it is time to apply the k-nearest neighbors algorithm.

library("class")
foundClass = knn(trn,tst,trueClass,k=3)

Remember that tst consists of 56 stars, so foundClass is a vector of that length.

foundClass

Here it so happens that there is not a single mistake!