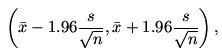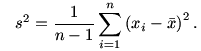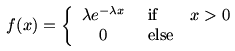Testing and Estimation
A simple example
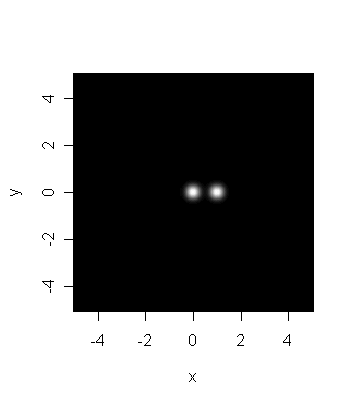
Consider the computer-generated picture below which is supposed to
mimic a
photograph taken by a low resolution telescope. Is it reasonable
to say that there are two distinct stars in the picture?
The next image is obtained by reducing the resolution of the
telescope. Each star is now more blurred. Indeed, their distance
in the picture is almost overwhelmed in the blur, and they appear
to be an elongated blur caused by a single star.
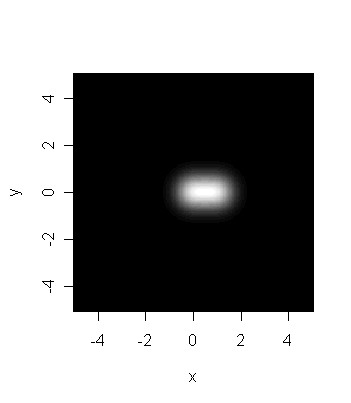
The last picture is is of the same two stars taken through a very
low resolution telescope. Based on this image alone there
is just no reason to believe that we are seeing two stars.
What we did just now is an informal version of a statistical test
of hypothesis. Each time we tried to answer the question ``Are
there two
stars or one?" based on a blurry picture. The two possibilities
``There is just one star'' as opposed to
``There are two stars''
are called two hypotheses. The simpler of the two gets the
name null hypothesis while the other is called the
alternative hypothesis. Here we shall take the first one
as the null, and the second one as the alternative hypothesis.
The blurry picture we use to make a decision is called the
statistical data (which always contains random
errors in the form of blur/noise). Notice how our final verdict
changes with the
amount of noise present in the data.
Let us follow the thought process that led us to a conclusion
based on the first picture. We first mentally made a note of the
amount
of blur. Next we imagined the centres of the bright blobs. If
there are two stars then the are most likely to be here. Now we
compare the distance between these centres and the amount of
blur present. If the distance seems too small compared to the
blur then we pass off the entire bundle as a single star.
This is precisely the idea behind most statistical tests. We
shall see this for the case of the two sample t-test.
Do Hyades stars differ in colour from the rest?
Recall in the Hipparcos data set we had 92 Hyades stars and 2586
non-Hyades stars. We want to test the null hypothesis
``The Hyades stars have the same colour as the non-Hyades stars''
versus the alternative hypothesis
``They have different colours.''
First let us get hold of the data for both the groups.
source("hyad.r")
colour = B.V
H = colour[HyadFilter]
nH = colour[!HyadFilter & !is.na(colour)]
m = length(H)
n = length(nH)
In the definition of nH above, we needed to exclude the NA
values. H is a list of m numbers and nH
is a list of n numbers.
First we shall make an estimate of the ``blur'' present in the
data. For this we shall compute the pooled estimate of standard
deviation.
blur.H = var(H)
blur.nH = var(nH)
blur.pool = ((m-1)*var(H) + (n-1)*var(nH))/(m+n-2)
Next we shall find the difference of the two means:
meanDiff = mean(H)-mean(nH)
Finally we have to compare the difference with the blur. One way
is to form their ratio.
(meanDiff/sqrt(blur.pool))/sqrt(1/m + 1/n)
This last factor (which is a constant) is there only for
technical reasons (you may think of it as a special constant to
make the ``units match'').
The important question now is ``Is this ratio small or large?''
For the image example we provided a subjective answer. But in
statistics we have an objective way to proceed. Before we see
that let us quickly learn a one-line shortcut to compute the above
ratio using the t.test function.
t.test(H,nH,var.eq=T) #we shall explain the "var.eq" soon
Do you see the ratio in the output? Also this output tells us
whether the ratio is to be considered small or large. It does so
in a somewhat diplomatic way using a number called the
p-value. Here the p-value is near 0, meaning
if the colours were really the same then then chance of observing
a ratio this large (or larger) is almost 0.
Typically, if the p-value is smaller than 0.05 then we reject the
null hypothesis. So we conclude that the mean of the colour of
the Hyades
stars is indeed different from that of the rest.
 |
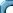 |  |  |
 |
A rule of thumb: For any statistical test (not just
t-test) accept the null hypothesis if and only if the
p-value is above 0.05. Such a test fails to recognise a true
null hypothesis at most 5% of the time.
|  |
 |  |  |
|
The var.eq=T option means we are assuming that the
colours of the Hyades and non-Hyades stars have more or less the
same variance. If we do not want to make this assumption, we
should simply write
t.test(H,nH)
 |
 |  |  |
 |
Use t.test for comparing means.
|  |
 |  |  |
|
Chi-squared tests for categorical data
Suppose that you are to summarise the result of a public
examination. It is not a reasonable to report the grades obtained
by each and every student in a summary report. Instead, we break
the range of marks into categories like first division, second
division, third division, failed etc. and then report the numbers
of students in each category. This gives an overall idea about
the distribution of grades.
The cut function in R does precisely this.
bvcat = cut(colour, breaks=c(-Inf,0.5,0.75,1,Inf))
Here we have broken the range of values of the B.V
variable into 4 categories:
(-Inf, 0.5], (0.5, 0.75], (0.75, 1] and (1,Inf).
The result (stored in bvcat) is a vector that
records the category in which each star falls.
bvcat
table(bvcat)
plot(bvcat)
It is possible to tabulate this information for Hyades and
non-Hyades stars in the same table.
table(bvcat,HyadFilter)
To perform a chi-squared test of the null hypothesis that the
true population proportions falling in the four categories are
the same for both the Hyades and non-Hyades stars, use the
chisq.test function:
chisq.test(bvcat,HyadFilter)
Since we already know these two groups differ with respect to the
B.V variable, the result of this test is not too
surprising. But
it does give a qualitatively different way to compare these two
distributions than simply comparing their means.
The test above is usually called a chi-squared test of
homogeneity. If we observe only one sample, but we wish to test
whether the categories occur in some pre-specified proportions, a
similar test (and the same R function) may be applied. In this
case, the test is usually called the chi-squared test of
goodness-of-fit. We shall see an example of this next.
Consider once again the Hipparcos data.
We want to know if the stars in the
Hipparcos survey come equally from all corners of the sky. In
fact, we shall focus our attention only on the RA
values.
First we shall break the range of RA into 20 equal intervals (each of
width 18 degrees), and find how many stars fall in each bin.
count = table(cut(RA,breaks=seq(0,360,len=20)))
chisq.test(count)
Kolmogorov-Smirnov Test
There is yet another way (a better way in many situations) to
perform the same test. This is called the Kolmogorov-Smirnov
test.
ks.test(RA,"punif",0,360)
Here punif is the name of the distribution with
which we are comparing the data. punif denoted the
uniform distribution, the range being from 0 to 360. Thus, here
we are testing if RA is taking all values from 0
to 360 with equal likelihood, or are some values being taken more
or less frequently.
The Kolmogorov-Smirnov test has the advantage that we do not need
to group the data into
categories as for the chi-squared test.
 |
 |  |  |
 |
Use chisq.test and ks.test for comparing
distributions.
|  |
 |  |  |
|
Estimation
Finding (or, rather, guessing about) the unknown based on
approximate information (data) is the aim of statistics. Testing
hypotheses is
one aspect of it where we seek to answer yes-no questions about
the unknown. The problem of estimation is about guessing the
values of unknown quantities.
There are many methods of estimation, but most start off with a
statistical model of the data. This is a statement of how
the observed data set is (probabilistically) linked with the
unknown quantity of interest.
For example, if I am asked to estimate p based on the data
Head, Head, Head, Tail, Tail, Head, Head, Tail, Head, Tail, Tail, Head
then I cannot make head-or-tail of the question. I need to link
this data set with p through a statement like
A coin with probability p was tossed 12 times and the data
set was the result.
This is a statistical model for the data. Now the problem of
estimating p from the data looks like a meaningful one.
 |
 |  |  |
 |
Statistical models provide the link between the observed data and
the unknown reality. They are indispensable in any statistical
analysis. Misspecification or over-simplification of the
statistical model is the most frequent cause behind misuse of
statistics.
|  |
 |  |  |
|
Estimation using R
You might be thinking that R has some in-built tool that can
solve all estimation problems. Well, there isn't. In fact, due to
the tremendous diversity among statistical models and estimation
methods no statistical software can have tools to cope
with all estimation problems. R tackles estimation
in three major ways.
- Many books/articles give formulae to estimate various
quantities. You may use R as a calculator to implement them.
With enough theoretical background you may be able to come up
with your own formulae that R will happily compute for you.
- Sometimes estimation problems lead to complicated
equations. R can solve such equations for you numerically.
- For some frequently used statistical methods (like
regression or time series analysis) R has the estimation methods
built into it.
To see estimation in action let us load the Hipparcos data set.
hip = read.table("HIP.dat",head=T)
attach(hip)
Vmag
If we assume the statistical model that the Vmag
variable has a normal distribution with unknown mean μ and
unknown variance σ2 then it is known from the literature
that a good estimator of μ is 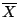 and a
95% confidence interval is
and a
95% confidence interval is
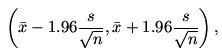
where
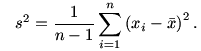
This means that the true value of μ will lie in this
interval with 95% chance. You may think of μ as
a peg on the wall and the confidence interval as a hoop thrown at
it. Then the hoop will miss the peg in only about 5% of
the cases.
| Exercise:
Find the estimate and confidence interval for μ based
on the observed values of Vmag using R as a calculator.
|
Next we shall see a less trivial example.
The data set comes from NASA's Swift satellite. The statistical
problem at hand is modeling the X-ray afterglow of gamma ray
bursts. First, read in the dataset:
dat = read.table("GRB.dat",head=T)
flux = dat[,2]
Suppose that it is known that the flux variable has
an Exponential distribution. This means that its density function
is of the form
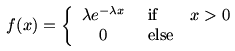
Here λ is a parameter, which must be positive. To
get a feel of the density function let us plot it for different
values of λ
x = seq(0,200,.1)
y = dexp(x,1)
plot(x,y,ty="l")
Now let us look at the histogram of the observed
flux values.
hist(flux)
The
problem is estimating λ based on the data may be
considered as finding a value of λ such that the
the density is as close as possible to the histogram.
We shall first try to achieve this interactively.
source("interact.r")
This should open a tiny window as shown below with a slider and a
button in
it.
 |
| Screenshot of the tiny window |
Move the slider to see how the density curve moves over the
histogram. Choose a position of the slider for which the density
curve appears to be a good approximation.
| Exercise:
It is known from the theory of Exponential distribution that
the Maximum Likelihood Estimate (MLE) of λ
is the reciprocal of the sample
mean
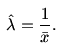
Compute this estimate using R and store it in a variable
called lambdaHat.
Draw the density curve on top of the
histogram using the following commands.
y = dexp(x,lambdaHat)
lines(x,y,col="blue")
|





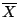 and a
95% confidence interval is
and a
95% confidence interval is