Principal Component Analysis

A simple example

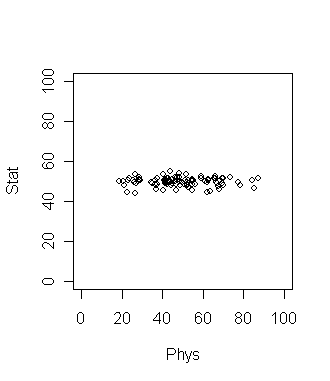
Consider 100 students with Physics and Statistics grades shown in the diagram below. The data set is in marks.dat.

If we want to compare among the students which grade should be a better discriminating factor? Physics or Statistics? Surely Physics, since the variation is larger there. This is a common situation in data analysis where the direction along which the data varies the most is of special importance.

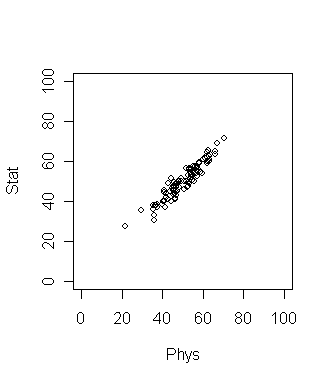
Now suppose that the plot looks like the following. What is the best way to compare the students now?

Here the direction of maximum variation is like a slanted straight line. This means we should take linear combination of the two grades to get the best result. In this simple data set the direction of maximum variation is more or less clear. But for many data sets (especially high dimensional ones) such visual inspection is not adequate or even possible! So we need an objective method to find such a direction. Principal Component Analysis (PCA) is one way to do this.

dat = read.table("marks.dat",head=T)
dim(dat)
names(dat)
pc = princomp(~Stat+Phys,dat)
pc$loading

Notice the somewhat non-intuitive syntax of the princomp function. The first argument is a so-called formula object in R (we have encountered this beast in the regression tutorial). In princomp the first argument must start with a ~ followed by a list of the variables (separated by plus signs).

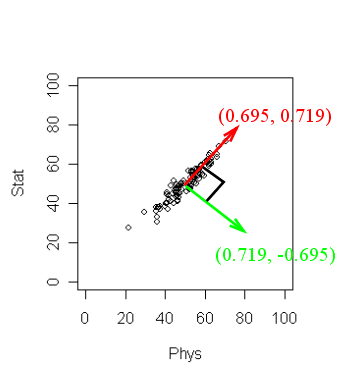
The output may not be readily obvious. The next diagram will help.

R has returned two principal components. (Two because we have two variables). These are a unit vector at right angles to each other. You may think of PCA as choosing a new coordinate system for the data, the principal components being the unit vectors along the axes. The first principal component gives the direction of the maximum spread of the data. The second gives the direction of maximum spread perpendicular to the first direction. These two directions are packed inside the matrix pc$loadings. Each column gives a direction. The direction of maximum spread (the first principal component) is in the first column, the next principal component in the second and so on.

There is yet more information. Type

pc

to learn the amount of spread of the data along the chosen directions. Here the spread along the first direction is 12.40. while that along the second is much smaller 1.98. These numbers are often not of main importance, it is their relative magnitude that matters.

To see all the stuff that is neatly tucked inside pc we can type

names(pc)

We shall not go into all these here. But one thing deserves mention: scores. These are the projections of the data points along the principal components. We have already mentioned that the principal components may be viewed as a new reference frame. Then the scores are the coordinates of the points w.r.t. this frame.

pc$scores

Higher dimensions

Most statisticians consider PCA a tool for reducing dimension of data. To see this consider the interactive 3D scatterplot below. It is possible to rotate this plot with the mouse. By rotating suitably we can see that the cloud of points is basically confined in a 2D plane. In other words, the data set is essentially 2D.

Drag the picture with the mouse

The same conclusion may be obtained by PCA. Here the first two components will be along the plane, while the third will be perpendicular to the plane. These are shown as the three lines.

Putting it to action

Now that we have seen how PCA can identify if the data cloud resides in a lower dimensional space, we are ready to apply our knowledge to astronomy. We shall work with the SDSS Quasar data set stored in the file SDSS_quasar.dat. First we prepare the data set for analysis.

quas = read.table("SDSS_quasar.dat",head=T)
dim(quas)
names(quas)
quas = na.omit(quas)
dim(quas)

Now we shall apply PCA.

pc = princomp(quas[,-1],scores=T)

The scores=T option will automatically compute the projections of the data along the principal component directions.

Before looking inside pc let us make a mental note of what information we should be looking for. We should look for the loadings (which are 22 mutually perpendicular directions in a 22-dimensional space). Each direction is represented by a unit vector with 22 components. So we have 22 times 22 = 484 numbers! Whew! We should also know the spread of the data cloud along each of the 22 directions. The spread along each direction is given by just a single number. So we have to just look at 22 numbers for this (lot less than 484). So we shall start by looking for these 22 numbers first. Type

pc

to see them. Well, some of these are much larger than the rest. To get an idea of the relative magnitudes, let us plot them.

plot(pc)

Incidentally, this plot is often called a screeplot, and R has a function with that name (it produces the same output as the plot command).

screeplot(pc)

By default, the spreads are shown as bars. Most textbooks, however, prefer to depict the same information as a line diagram:

screeplot(pc,type="lines")

The term ``scree'' refers to pebbles lying around the base of a cliff, and a screeplot drawn with lines makes the analogy clear. But one should not forget that the lines do not have any significance. The points are the only important things.

We can see from the screeplot that only the first 2 components account for the bulk. In other words, the 22-dimensional data cloud essentially resides in just a 2D plane! Which is that plane? The answer lies in the first two columns of pc$loadings.

pc$loading[,1:2]

These give two mutually perpendicular unit vectors defining the plane. To make sure that this is indeed the case you may check as

M = pc$loading[,1:2]
t(M) %*% M #should ideally produce the 2 by 2 identity matrix

You might like to project the entire data set onto this plane.

plot(pc$scores[,1],pc$scores[,2],pch=".")

This is how the data cloud looks like in that magic plane in 22-dimensional space. And with my limited astronomy knowledge I have no idea why these look like this!!! (An astronomy student had once told me that this pattern has to do something with the way the survey was conducted in outer space.)

Peeping behind the scree...

It may be of some interest to know how PCA works. We shall not go into all the nitty gritty details, but the basic idea is not too hard to grasp, if you know eigen values and eigen vectors.

What PCA does is, roughly speaking, computing the eigen values and eigen vectors of the covariance matrix of the data. A detailed exposition of why that is done is beyond the scope of this tutorial. But we may use R's eigen analysis tools to hack a rough imitation of princomp ourselves. We shall take the students' grades data as our running example.

First compute the covariance matrix.

dat = read.table("marks.dat",head=T)
covar = cov(dat)

Next compute the eigen values and vectors:

eig = eigen(covar)

Now compare:

val = eig$values
sqrt(val)
pc = princomp(~Stat+Phys,dat)
pc

The values will not match exactly as there are more bells and whistles inside princomp than I have cared to divulge here. But still the results are comparable.

A better way

The princomp function is numerically less stable than prcomp which is a better alternative. However, its output structure differs somewhat from that for princomp.

Exercise: Read the help on prcomp and redo the above computation on the SDSS quasar data using this function. [Solution]