Time Series Analysis

Introduction

A time series is a data set collected over time where we suspect some evolution with time. However, 10 CCD bias plates taken over 5 minutes do not qualify as time series data, because we do not expect to have any time-dependent signal embedded in them. The differences between the 10 images are purely random without any temporal evolution. On the other hand for a long 2-hour session we may very well suspect that the CCD is drifting away from its ideal behaviour. So CCD biases taken every 15 minutes over 2 hours do constitute a time series.

A notation:

Something that changes with time (t) is denoted as a function f(t). We are all familiar with this notation.
Something that changes with chance is denoted by f(w), where the symbol w stands for ``chance''. It is just a notation, not a variable. In a sense w is the sum total of all effects whose presence cannot be measured but is felt.
In a time series we have a quantity that changes both with time as well as chance. So we use the notation X(t,w).

What is special about time series?

A very powerful weapon to tackle random variation is to take repeated measurements. But for a time series that is not possible because we cannot go back in time to take a fresh measurement of past values. So we need different techniques. These techniques start out by postulating a mechanism of how time and chance influence the data.

Role of time: This is usually determined by the underlying physics where everything is assumed known except for a few unknown parameters.
Role of chance: Chance enters into the picture either as intrinsic randomness (e.g., the experimenter's ignorance or quantum phenomena) or as measurement error.

A simple situation: No intrinsic randomness

Here the sole randomness in the set up is due to measurement errors. A commonly used model for this scenario is

X(t,w) = f(t) + e(w),

where the form of the time-dependent part f(t) is governed by the physical model. It is not random. The random error term e(w) is assumed free of time. This assumption is reasonable when the measuring instrument is calibrated frequently.

A popular example of such a model is the broken power law.

Broken power law

R does not have any ready made command to fit a broken power law. So let us write one program to do so. Our running example will use an IR data set about GRB030329 from Bloom (2003).

dat = read.table('bloom.dat')

The first column is time in days,and the second column is the magnitude.

x = log(dat[,1])
y = dat[,2]
plot(x,y)

First we shall choose a break point say at (A,B). Then we shall fit the best broken power law (which is just a broken linear law after taking logarithm) with the knee at that point. Since we have already fixed the knee, all that this fitting requires us to choose are the two slopes to be used on the two sides of the knee.

For this we shift our origin to (A,B) by subtracting A from x, and B from y. To explain the steps we shall take (arbitrarily) A=1.5 and B=17. We shall soon learn how to choose A and B optimally.

A = 1.5
B = 17
xnew = x - A
ynew = y - B

Next we pick all the points to the left of the knee

left = xnew < 0
xleft = xnew[left]
yleft = ynew[left]

Similarly, we also collect all the points to the right:

xright = xnew[!left]
yright = ynew[!left]

Next we have to fit a line through the origin (which is now at (A,B)) to the left hand points, and then separately to the right hand points. This will give us the best broken power law with the knee constrained to be at (a,b).

leftfit = lm(yleft ~ xleft - 1)
rightfit = lm(yright ~ xright - 1)

How good is this fit? We can assess this visually by just drawing the two lines.

leftslope = leftfit$coef
rightslope = rightfit$coef

abline(a=B - leftslope*A, b= leftslope,col='blue')
abline(a=B - rightslope*A, b= rightslope,col='red')

More objectively, the goodness of fit can be measured by the sum of the squares of all the residuals.

sum(leftfit$resid ^ 2) + sum(rightfit$resid ^ 2)

We have to choose the knee position (A,B) to minimise this error. A good way to proceed at this stage is to differentiate the error w.r.t. B, equate the derivative to 0, and so on. (Incidentally, the error is not differentiable w.r.t. A.) But a quick way is to take a grid of values for (A,B), compute the error for each value, and then choose the minimum. Here is some R code to implement this grid search.

agrid = seq(1.2,2.5,0.1)
bgrid = seq(15.5,19.5,0.1)
error = matrix(0,length(agrid),length(bgrid))
for(i in 1:length(agrid)) {
  for(j in 1:length(bgrid)) {
    A = agrid[i]
    B = bgrid[j]
    xnew = x - A
    ynew = y - B
    left = xnew < 0
    xleft = xnew[left]
    yleft = ynew[left]
    xright = xnew[!left]
    yright = ynew[!left]
    fitleft = lm(yleft ~ xleft - 1)
    fitright = lm(yright ~ xright - 1)

    error[i,j] = sum(fitleft$res ^ 2)+sum(fitright$res ^ 2)
  }
}
persp(agrid,bgrid,error)

Now we try to find the minimum error.

minpos = which.min(error)
row = (minpos-1)%%nrow(error)+1
col = floor((minpos-1)/nrow(error))+1
A = agrid[row]
B = bgrid[col]

Finally let's plot the fitted line.

plot(x,y)
points(A,B,pch=22)
xnew = x - A
ynew = y - B
left = xnew<0
xleft = xnew[left]
yleft = ynew[left]
xright = xnew[!left]
yright = ynew[!left]
leftslope = lm(yleft ~ xleft - 1)$coef
rightslope = lm(yright ~ xright - 1)$coef
abline(a=B - leftslope*A ,b= leftslope,col='blue')
abline(a=B - rightslope*A ,b= rightslope,col='red')

When intrinsic randomness is present

In most non-trivial problems intrinsic randomness is present, and we cannot split X(t,w) simply into two parts, one involving only t and the other involving only w. We need a more complex way to combine the effects of t and w.

In order to do this we need to have a clear idea as to the aim of our analysis. Typically the two major aims are

Understanding the structure of the series: e.g., The period of waxing and waning of the brightness of a star gives us valuable information about exo-planets around it.
Predicting future values: In many applications of statistics (e.g., in econometrics) this is the primary aim. But this is only of secondary importance in astronomy.

A case study: Sunspots

Understanding the structure of a time series primarily means detecting cycles in it. Consider the sunspot data as an example.

dat = read.table("sspot.dat",head=T)
plot(ts(dat[,1],freq=12*12,start=c(1749,1)),ty="l",ylab="sunspots (monthly means)")

We can see a cyclical pattern. We want to find its period using Fourier Analysis/Spectral Analysis. This is the fundamental idea behind spectroscopy. But there is an important distinction between that and what we are going to do now.

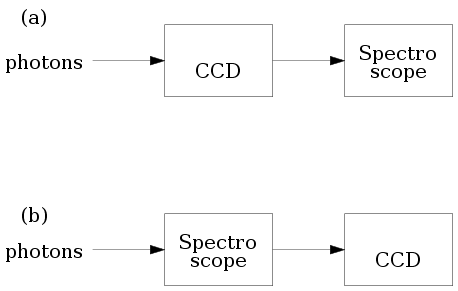
Consider the two configurations for using a spectroscope. In (a) the photons are allowed to impinge on the CCD first and the CCD signals are fed into the spectroscope.

In (b) the light is first fed to the spectroscope, and CCD comes after that. We all know that the former configuration is of no practical value, because CCD's are slow devices compared to frequency of light waves. Thus CCD's lose all color information. So we need to input the raw light to the spectroscope.

In our statistical analysis however we shall use the configuration shown in (a). The spectroscope here will be a software algorithm that needs numerical input. We shall be working with cycles of large enough periods, so that the slow response of CCD's will pose no problem.

The basic math behind Fourier Transforms (or Fast Fourier Transforms, as its commonly used efficient implementation is called) is beyond the scope of this tutorial. We shall nevertheless remind ourselves of the concept using a toy example.

t = 1:200 
y1 = sin(2*pi*t/20)
y2 = sin(2*pi*t/12)
y3 = sin(2*pi*t/25)

y123 = y1+y2+y3


par(mfrow=c(2,1))
plot(t,y1,ty="l")
plot(t,y2,ty="l")
plot(t,y3,ty="l")
plot(t,y123,ty="l")

Notice how irregular the plot of y123 looks even though it is just a smooth mathematical function. Mere inspection has no hope of ever finding that it is actually made of 3 different sinusoids! Now we shall feed this into our software spectroscope.

par(mfrow=c(2,1))
sp = spectrum(y123)
plot(sp$freq, sp$spec, ty="l")

Observe how the 3 components clearly stand out now!

Now we are in a position to apply our software spectroscope to the sunspot data.

dat = read.table("sspot.dat",head=T)
names(dat)
attach(dat)


plot(sspot,ty="l")

sp = spectrum(sspot)
plot(sp$freq,sp$spec,ty="l")

We are interested in the strongest period present. This is indicated by the highest peak. We can find it by inspection, or we may let R find it for us:

index = which.max(sp$spec)
1/sp$freq[index]

Unevenly sampled data

Its appealing mathematical properties notwithstanding, the Fast Fourier Transformation suffers from one great drawback: its expects the data points to evenly spaced along the time line. But in an observational science like astronomy, where physical conditions like clouds govern availability of data, such data sets are extremely rare. Various modifications to spectral analysis have been suggested to cope with this situation. We shall discuss one of them here: the Lomb-Scargle approach, which is available as a collection of R functions freely downloadable from the web. A good reference for the implementation details is Numerical Recipes in C by Press et al. To learn the details of R version please see here. The following example is taken from that page, and is explained there.

source("LombScargle.R")

unit = "hour" # hourly data
set.seed(19)    # make this example reproducible

time = sort( runif(48, 0, 48) )

Expression = cos(2*pi*time/24 + pi/3) # 24 hour period

M = 4*length(time) # often 2 or 4

# Use test frequencies corresponding to 
# periods from 8 hours to 96 hours 
TestFrequencies = (1/96) + (1/8 - 1/96) * (1:M / M)

# Use Horne & Baliunas' estimate of independent frequencies 
Nindependent = NHorneBaliunas(length(Expression))

ComputeAndPlotLombScargle(time, Expression,
  TestFrequencies, Nindependent,
  "Cosine Curve (24 hour period)")

Prediction

Predicting a time series is not often the most important concern in astronomy. Understanding the forces governing the dynamics of a time series is of more importance to the observational astronomer. Nevertheless prediction has its uses, and we shall now learn about some techniques that are geared towards this aim.


	Any prediction technique needs to assume, fit and extrapolate some temporal pattern based on the data. It must be borne in mind that such a temporal pattern is purely for the purpose of prediction. Trying to attach structural significance to it may lead to misleading conclusions. Compare the situation with that of approximating a smooth function with splines. The coefficients used in the spline curves have usually no physical significance.

Holt-Winters method

This is a very simple (if crude) technique that assumes that the time series is composed of a slowly varying signal plus a cyclical fluctuation of known period plus random noise.

The Holt-Winters method is basically a tracking method that tracks the signal and cyclical fluctuation over time using a feedback loop. To understand the algorithm imagine how a robot arm that is capable of only linear movement can trace a curve. It makes a sequence of small linear steps updating the slope at each point based on feedback from its sensor.

Similarly, the Holt-Winters method approximates a complicated time series using a linear component and a cyclical term:

a + b h + s_t+h ,

where the linear coefficients a,b and the cyclical term s_t+h are automatically updated using three different feedback loops. These three loops are controlled by three tuning parameters alpha, beta and gamma. These take values between 0 and 1. If a tuning parameter is chosen to be FALSE then the corresponding feedback loop is switched off. The following command, for example, applies the Holt-Winters method to the sun spot data without any cyclical term:

hw = HoltWinters(sspot, gamma = FALSE)

To predict the next 200 observations we can use

p = predict(hw,200)


par(mfrow=c(1,1))
ts.plot(ts(sspot),p,col=c("black","red"))

Of course, this is pretty silly prediction, since we suppressed the cyclical fluctuations by force. A more reasonable prediction may be had if we allow default values for all the three tuning parameters (the defaults are not fixed values, they are computed by R based on the data).

hw = HoltWinters(sspot)

Oops! R complains because it has no idea about the periodicity.

sspot = ts(sspot, freq=12*12)
hw = HoltWinters(sspot)
p = predict(hw,200)


ts.plot(sspot,p,col=c("black","red"))

This prediction looks much better. But it must be borne in mind that it is a very crude method, and does not produce any error bar. Its absolute simplicity makes it an ideal choice for one-step-ahead predictions computed online (i.e., where the prediction is updated at each step as more data arrive).

Box-Jenkin's method

The method that we are now going to learn is the most popular statistical method of time series analysis, though its applicability to problems in astronomy is somewhat limited. At the heart of this method sits the somewhat tricky concept of a stationary time series. We shall first acquaint ourselves with this concept through some examples.

Stationarity

In all the time series models encountered so far we have some idea about the temporal evolution of the series (like presence of some linear trend and/or cyclical fluctuations etc). We usually have such an idea from prior knowledge about the physical process generating the data. If we are looking at the light curve of a star with an exo-planet we expect to see periodic ups and downs. But what if we do not have any such prior idea? Then we assume that the distribution of the random variable X(t,w) is free of t. Such a time series is called stationary.

One must not forget that stationarity is not a property of the data per se, rather it describes the state of background information we have about the data. When we say

"a particular time series is stationary"

we are saying that

"we have no background information that leads us to believe that the random behaviour of the series evolves with time."

Considered superficially this may seem to indicate that there is no useful temporal information in the series, and that no meaningful prediction is possible. That this naive interpretation is not correct is the most remarkable fact about Box-Jenkins modelling. Before going into complications let us realise this point using a simple example.

First consider some white noise, which is the simplest example of stationary time series.

x = rnorm(100)
plot(x,ty='l')

Next let us apply a 3-point moving average to the white noise.

The following R code achieves this:

y = numeric(98)
for(i in 1:98) y[i] = mean(x[i:(i+2)])

The averaging introduces correlation among the y's. But convince yourself that they are still stationary.

plot(y,ty='l')

The plot shows a somewhat regular wavy pattern that might very well be exploited for the purpose of prediction. This illustrates the oft encountered scenario where the distribution does not evolve with time, but particular realisations do!

AutoRegressive Moving Average (ARMA) model

Many time series data are modeled as

This rather hairy object is indeed less pretentious than it looks. Here X_t is the value of the series at time t. The model says that part of the randomness in X_t comes from its dependence on the past values: X_t-1,...,X_t-p; and the rest comes from fresh random errors ε_t,...,ε_t-q from now and the q most recent time points.

Viewed in this light, the model (which bears the impressive name ARMA(p,q)) says what is applicable in general to most time series. Exactly how the past X's and the ε's influence X_t is governed by the coefficients φ's and θ's, which we shall estimate from the data. The only arbitrary part in the model seems to the choice of p and q. While it is reasonable to assume that X_t is influenced by the past values X_t-1,...,X_t-p, how do we exactly choose p? The same question may be asked for q.

To make informed guesses about p and q based on data, one usually computes two functions called the Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) from the data. Both these functions have somewhat complicated formulae that do not shed much light on their nature. So instead we shall take an intuitive approach.

ACF

When we want to measure the degree of association between two quantities a common method is to collect data about them, and compute the correlation. Suppose that we are interested in knowing how much association is there between an observation in a time series and the observation immediately preceding it. The simplest way would be consider all consecutive pairs in the time series data, and compute the correlation based on them. This is basically what is done in time series analysis, and the resulting correlation is called the autocorrelation at lag 1.

Had we paired each observation with the one 2 time points behind it, then the resulting correlation would have been called autocorrelation at lag 2.

The autocorrelation function (ACF) is a function γ(h) for h=1,2,... where γ(h) is the autocorrelation at lag h. One main utility of the ACF is for guessing the value of q. For an ARMA(0,q) model (which is also called an MA(q) model) typically the first q values of the ACF tend to be large, while the remaining are smaller in comparison. In practice it is often not clear at all how to decide which ACF's are large and which are not. So the ACF only provides a very rough guidance, that we shall learn to polish soon.

To compute ACF for a time series data set we can use the acf command as follows.

acf(sspot)

Well, here the ACF is dying out, but rather slowly. This is indicative of p≠0 and q=0. We shall get a further confirmation for this guess when we consider the partial autocorrelation function below.

PACF

Correlation measures association between two variables. However, it does not tell us if the association is direct or indirect. An example if indirect association is where two variables X,Y are both associated with a common third variable Z. For example, temperature (X) outside the telescope may found to have association with the amount (Y) of noise in the CCD. A scientist may guess that the association occurs indirectly via the temperature (Z) of the CCD unit. Merely finding the correlation between X and Y is not enough to test the scientist's guess. We can, instead, wrap the CCD unit in very good temperature control system (making Z a rock-solid constant) and then compute the correlation between X and Y. If now the correlation drops down to zero, we indeed have reason to support the scientist's guess. The correlation we computed just now is called the partial correlation between X and Y fixing Z. It measures the association between X and Y other than via Z.

In the context of time series we compute partial correlation between X_t and X_t+h fixing all the X's inbetween. This is the value partial autocorrelation function (PACF) at lag h.

Just as the ACF helps us to guess q, the PACF helps us guess the value of p: the first p PACF's tend to be larger than the rest.

The R command pacf computes PACF (surprise!).

pacf(sspot)

The two blue margins provide an aid to deciding whether a PACF value is "large" or not. Values within or barely peeping out of the margins may be considered "large", the rest being "small".

Our plot indicates that p=5 and q=0 might be good guesses to start with.

Fitting the model

Once we have made a rough guess about p and q we need to estimate the coefficients θ's and φ's. The elaborate mathematical machinery required for this is conveniently hidden from our view by the arima command of R. Note the extra `i' in arima. Actually R works with a more general model called ARIMA (AutoRegressiive Integrated Moving Average) of which ARMA is a special case. Here is an example of the arima command in use:

fit=arima(sspot,order=c(5,0,0))

Note the triple c(5,0,0). The first 5 is the value of p, the last 0 is that of q. The middle 0 is not used in an ARMA model (it is used in the more general ARIMA model).

This rather benign-looking command launches a lot of computation in the background, and if successful, dumps the results in the variable fit.

There are various things that we can do with this object. Possibly the first thing that we should do is to take a look at what is inside it.

fit

How good is the fitted model?

But before we put it to any serious use like prediction, we should better make sure that it is indeed a good fit. One way to check this is by plotting the residuals:

plot(fit$resid)

Preferably the plot should show a series of small values without any pattern. Any pattern in the residual plot indicates that the fitted model has been inadequate to explain that pattern. This is the case here. The regular periodic fluctuations are too strong to be called "patternless".

Polishing the model

What we do to remedy a bad fit depends heavily on the particular data set, and is something of an art. We shall point out two methods here:

Box-Cox transformation

The model fitting relies heavily on the normality of the data. Let's check if that is a suspect here.

hist(sspot)

Well, the plot is extremely skewed. A simple remedy to cure te skewness is to apply a Box-Cox transform to the data. Box-Cox transforms constitute a family of one-to-one (i.e., lossless) transforms that allow the user to change the skewness present in a dataset. They are defined as

By choosing λ appropriately one may change the shape of the histogram. Some trial and error are needed before a good value of λ is found.

lambda=0.1; hist((sspot ^ lambda - 1)/(lambda-1))

Notice how we have used a ; as a separator to pack two commands in one line. This is useful when we want to replay multiple commands repeatedly. Replay the line a number of times, each time changing the value of λ. The value 0.35 looks like a good value. Let's repeat the analysis with the transformed data:

sspot1 = (sspot ^ 0.35 - 1)/(0.35-1)
fit1 = arima(sspot1,order=c(5,0,0))
plot(fit1$resid)

Much better this time!

Comaparing models

One thing to try out is to change p or q slightly and see if the fit improves. This comparison is facilitated by the Akaike Information Criterion (AIC) which is a summarisation of the goodness of fit of the fitted model in terms of a single number. If we have two competing models for the same data set, then the one with the smaller AIC is the better fit. The command to compute AIC in R for the fitted model stored in fit is

AIC(fit)

AIC cannot be compared for models based on different data sets. As a result there is no universal threshold against which to rate a single AIC value on its own.

It may happen that no ARMA model fits the data at hand. In this case we have to migrate to some different (and more complicated) class of models. And above all, we must not forget that there are just not enough types of models in statistics to fit all kinds of time series data occurring in practice!